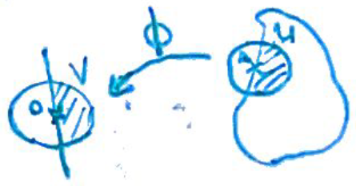Ouvert régulier \(\Omega\subset{\Bbb R}^d\)
Ouvert pour lequel \(\forall x\in\partial\Omega\), \(\exists U\ni x\), \(\exists V\ni 0\)
Ouverts de \({\Bbb R}^d\), \(\exists\phi\in\mathcal C^\infty(U,V)\) un
Difféomorphisme tel que $$\phi(\Omega\cap U)=(]0,+\infty[\times{\Bbb R}^{d-1})\cap V.$$
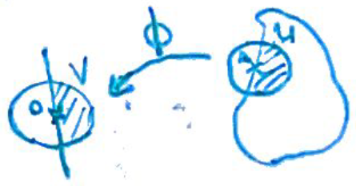
- si \(\Omega\) est un ouvert régulier et \(s\in{\Bbb N},p\in[1,+\infty]\), alors on peut prolonger les fonctions d'un Espace de Sobolev d'un ouvert vers tout l'espace, de façon linéaire et continue : $$\exists P:W^{s,p}(\Omega)\to W^{s,p}({\Bbb R}^d)\text{ linéaire continue},\forall u\in W^{s,p}(\Omega),\quad Pu\rvert_{\Omega}=u$$
- si \(\Omega\) est un ouvert régulier, \(s\in{\Bbb N},p\in[1,+\infty[\), alors \(\{\varphi\rvert_\Omega\mid\varphi\in\mathcal D({\Bbb R}^d)\}\) est dense dans \(W^{s,p}(\Omega)\)